袁旸洋 / YUAN Yang-yang
成玉宁 / CHENG Yu-ning
摘要:风景环境的道路选线不仅需要综合研究地形、植被、水体等多种因素,而且应满足生态、功能、工程量合理、审美等多项要求,是一项多目标的系统性工程。参数化方法的使用为风景环境道路选线提供了可靠的科学依据,较之于传统的凭经验选线方法更为科学、准确、高效、可操作性强。基于ArcGIS软件平台的道路选线算法,构建了参数化风景环境道路选线模型,并以南京牛首山景区北部片区为例讨论参数化风景环境道路选线模型的应用。
关键词:风景园林;参数化;风景环境;道路选线;模型构建
Abstract: Route selection in landscape environment not only needs to comprehensively research on a variety of factors, such as topography, vegetation, water, but also should satisfy the ecological, functional, quantitative, and aesthetic requirements. So it is a multiobjective systemic engineering. Compared with the experiential method, the parametric method provides the reliable scientific basis for route selection in landscape environment, and it is much more scientific, accurate and efficient. This paper discusses the route selection algorithm based on ArcGIS software platform, and builds the parametric model of landscape environment route selection. Then, taking the northern area of Nanjing Niushou Mountain Scenic Area as an example, the paper discusses the application of parameterized model of landscape environment route selection.
Key words: landscape architecture; parametric; landscape environment; route selection; model building
《风景名胜区规划规范》(GB 50298-1999)就交通及道路的规划提出:方便可靠和合适风景区特点,并形成合理的网络系统;还应当合理利用地形,因地制宜地选线,同当地景观和环境相配合,避免深挖高填。风景环境的道路不单纯追求捷径,而是需要与各景观节点形成良好的串联关系,以景观节点为线路控制点,形成合理的交通网络系统。通常风景环境地形地貌较为复杂,且有生态敏感区域存在。因而,风景环境道路的选线应与地形地貌相契合,线形应灵活多变,结合场所条件可适当弯曲、起伏,同时尽量避免过大的土方工程,减少对风景环境的人为扰动。因地制宜的道路不仅能够为游人提供交通,并且是风景的组成部分。风景环境的道路选线需要综合研究地形、植被、水体等多种因素,并满足生态、工程量、功能、审美等多项要求,是一项多目标的系统性工程。
1 风景环境道路的选线
1.1 传统的道路选线方法
传统的道路选线有赖于设计人员通过对选线区域的地形等因素加以分析,于较大比例的地形图上进行计算并绘制道路选线。然后根据图纸方案进行实地勘测,逐段放线,经过反复的比较之后确定一个较为经济、合理的方案。手工选线的方法不仅需要设计人员具有丰富的实践经验及技术水平,且费时费力,对选线的经济及合理性也只能通过主观经验形成模糊的判断。同一条件下,往往随设计人员的经验、水平与手法不同,其结论具有或然性。
1.2 基于ArcGIS平台的道路选线方法
航测技术、计算机技术和信息技术等科学技术的发展为道路选线提供了较之传统方法更为有效的手段,道路选线方法进入继实地选线、航测选线之后的第三发展阶段,即自动化选线阶段。1958年美国麻省理工学院的米勒(Charles Leslie Miller)教授率先提出了基于数字地形模型(DTM)以实现公路选线过程自动化。
根据风景环境道路选线的特点,本研究关于道路选线模型借鉴综合成本最短路径算法模型。该模型基于数字高程模型(DEM),通过GIS栅格数据及其邻接关系,进行空间最优路径模拟与运算,对坡度分级费用、最大坡长、最大纵坡和选线范围等限制条件展开研究,利用最短路径分析工具、运用成本栅格矩阵法计算出最优路径。该模型的优势首先在于基于综合成本图的算法模型能够较好地满足景园道路对于土方、纵坡、线型等基本要求,同时能够有效地绕行生态敏感区、径流密集区等限制性区域;其次,通过评价将影响选线的各种因子转换为基本“成本”地图,可以充分利用诸如生态敏感性分区等景园规划设计前期分析的成果,转化为选线的影响因子基础图;同时,该模型工具简单,操作十分简便。
2 基于ArcGIS的道路选线算法
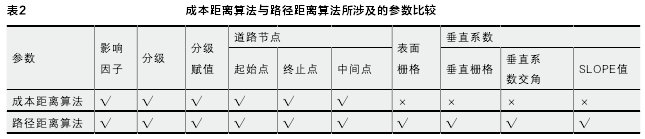
GIS进行空间数据分析主要是基于栅格模型与矢量模型2种表示模型。道路选线利用了ArcGIS中的距离工具,进行计算与分析的对象为栅格模型,涉及成本距离、路径距离与成本路径3种算法。
2.1 成本距离算法
“距离”一词表述的是2个实体之间的远近程度,空间分析中的距离除包含两点间直线长度之外,还包括了从一点移动到另一点所遇到的“阻力”或者“代价”,体现为两点间距离的一种函数关系。在GIS选线算法中,“成本”的概念不同于日常,并不局限于“以货币计量的价值”。“成本距离”指的是空间中从一点移动到另一点所耗费的“成本”或者“代价”,需要通过成本距离加权函数进行计算。以步行为例,在公园游步道上行走比乡村泥泞的小道更加容易,即便行走的直线距离相同,所遇到的阻力也是不同的。成本距离加权函数能够计算出每个栅格到距离最近、成本最低源的最少累加成本,可得出成本方向数据与成本分配数据。其中,成本方向数据表示了从每一单元出发,沿着最低累计成本路径到达最近源的具体路线。
2.2 路径距离算法
路径距离算法与成本距离算法相比较而言,两者都可以计算从某个源到栅格表面上各位置的最小累积行程成本。然而,路径距离算法能够考虑更多复杂的因素,最突出的是实际移动距离与水平、垂直因素均参与运算。汽车在行驶时,路面的摩擦、风阻均会对移动产生阻力。同时汽车在起伏路面的行驶中所移动的距离要大于两点间的直线距离。以上均为影响运动的因素,较之成本距离算法,路径距离算法能够将地形的起伏、坡度均以参数的方式加入运算过程,更适用于风景环境的道路选线。
路径距离算法中,最重要的参数之一为高程栅格,利用表面栅格来计算定从一个像元行进到下一个像元的实际表面距离,与平面(“直线”)距离相比更贴合人或者车在风景环境中的运动情况。据此,表面越不平坦时,行程距离也随之变大,距离越大,意味着发生的成本越多,与之对应,地形起伏过大的地段不适宜道路的建设。另一个重要的参数为垂直系数。垂直系数反映的为坡度和移动阻力的关系,即垂直系数越大表明坡度越陡,移动越困难。根据道路设计的要求,景园道路设计的纵坡比城市道路、公路能够适当放宽。但坡度大于30%的地段仍不适宜建设,这一参数能够通过垂直系数来加以反映。图1反映的是在切削角±90°,SOLPE(修正斜率)分别为1/90(0.011 11)、1/45(0.022 22)、1/30(0.033 33)时垂直系数(VF)与垂直相对移动角度(VRMA)之间线性对称的函数关系比较。对于景园规划设计而言,坡度体现为与水平面所呈的角度,不论正相关抑或负相关亦以坡度的形式存在,均需要垂直系数对移动的成本进行修正,因此在运算时选取线性对称函数。由于坡度大于30%的区域不适合建设,与之对应将切削角设定为±30°,即坡度大于30°的区域移动的困难程度趋于无限。
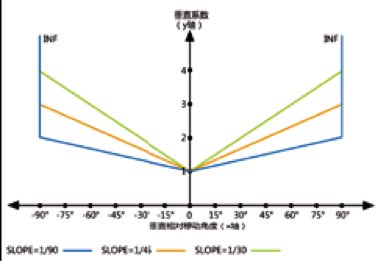
图1 不同SLOPE值对应的对称线性函数垂直系数图(垂直参数交角=±90°)
2.3 成本路径算法
成本距离算法与路径距离算法均以某个源为依据,计算该源到栅格表面上各位置的最小累积行程成本。成本路径的计算便是在上述基础之上通过最短路径函数获取从一个源或一组源出发,到达一个目标地或一组目标地的最小成本路径。GIS中的 “最短路径”不仅仅指的是一般意义上的“直线最短”,在加入“成本”进行运算之后,“最短路径”体现为最低“成本”之下的最短。根据GIS函数计算的特点,生成的路径为最小成本前提下的最短路径,由于计算方式所限,既有的成本路径选线算法难以满足风景环境的实际。因此,需要在现有算法的基础上,遵循风景环境道路的特点对选线参数加以针对性的调整与优化。
3 参数化风景环境道路选线模型的构建
基于成本距离或路径距离算法、成本路径算法,构建景园规划设计道路选线模型(图2)。与2种算法参加运算的顺序一致,模型共分为2个参数化运算部分以及最后的人机交互部分:综合成本的计算、最优路径的生成以及路径的筛选与优化。首先,综合成本的计算中包括了3个过程,依次为:影响因子的判定、因子权重的判定、因子的叠加分析,以上3个过程在GIS中完成,得到综合成本图作为参数输入到下一个运算阶段。其次,成本路径运算阶段中,道路节点与综合成本图作为参数输入,通过给定条件情况下的最短路径分析得出初级最优选线。最后,通过人机交互的方式对初级选线进行筛选与优化,剔除不合理的路径,得到最终的道路选线。
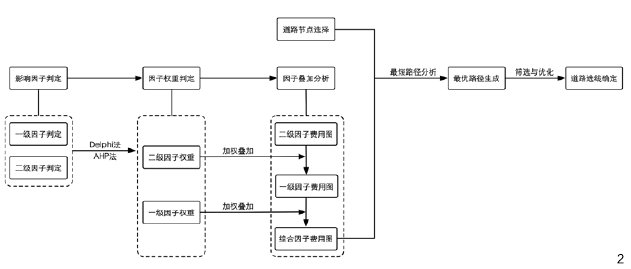
3.1 影响因子的判断
影响道路选线方案的因素多且复杂,不同地域的情况各异,规划设计定位各不相同,对道路选线要求的侧重点不同,因而需要针对场所特点确定影响因子。就绝大多数情况而言,道路选线需要满足的条件可以归结为3类:第一类属于控制点因素,控制点因素包括起点、端点和中间的必经点,也决定了路线的长度;第二类因素与地理空间位置相关,如地形地貌、地质条件、水文条件等;第三类为限制性因素,景园规划设计中最为重要的限制性因素为生态敏感区,除此之外还包括建筑、各类设施、植被等保留的地物,为道路选线提供了限制性范围。
3.2 因子权重的确定
在景观环境的道路选线中坡度、起伏度、生态敏感区、汇水区等均是需要考虑的因子,因而成为道路建设的“成本”。表1展示了通常情况下道路选线所涉及的影响因子。在影响因子确定后,利用德尔菲法、层次分析法对因子的权重进行判定。不同场所的道路选线影响因子及因子的权重各不相同。一般来说,坡度、起伏度等直接对道路营建起决定性作用的因子权重较大。风景环境中允许部分道路穿越水面,以景观桥梁的形式丰富空间层次,为游人提供不同的游览体验,因此水域因子的权重不宜过大。就现状道路与保留设施进行道路的建设无疑成本较低,对环境的扰动较小,但是若两者的权重值设置过高会对选线的正确性产生一定影响。因子的权重作为综合成本图生成的重要参数,对于整个选线的合理性有着直接的作用,权重值的不合理设置会直接导致选线的失败,因此需要在正确评估的基础上确定各因子的权重。同时,在初步选线的基础上进行分析,如若合理性不佳,则应重新计算综合成本图,即对权重确定过程进行反馈,重新分配各因子的权重。
3.3 因子的叠加分析
在各影响因子权重确定的基础上,利用ArcGIS软件对各因子进行重分类。这一过程的目的在于将各性质不同的因子进行无量纲化,并统一分级赋值,将各因子纳入同一评价体系,为叠合做准备。将重分类图进行叠合便得到综合成本图,是选线的基础图纸。由于综合成本分级与各因子分级一致,因此因子的分级与赋值会直接影响综合成本。分级决定了综合成本的层次标准,层次越丰富所对应的成本“值”数越多,为计算提供的可能性越丰富。根据算法的计算规则,对应的选线结果越准确。由以上分析可知,影响因子的选择、因子权重的判断及单因子的分级均会对最优路径的选择产生影响。
3.4 道路节点的选择
道路节点指的是道路的起始点、终止点以及中间的必经点。道路的节点与上一阶段生成的综合成本图将作为参数,参加成本距离、路径距离与成本路径的运算。风景环境多为中、大尺度区域,故而道路系统通常为网状,区域需要设置多个出入口以便于交通组织。鉴于以上特点,景观环境道路节点的选择与一般城市道路、公路有较大不同。
首先为道路起始点及终止点的确定。根据成本距离或路径距离的算法,起始点将作为参数输入。整个设计区域的出入口一般设为道路起始点,作为联系外部交通与内部交通的转换节点。由于有多个出入口,主入口作为必然作为道路的起始点参与选线运算,辅助出入口作为辅助起始点参与整个路网的形成。根据风景环境道路的网状特点,不存在一般意义上的道路终止点。项目选址过程所确定的项目位置须有道路加以连通,因此可认为项目均与道路起始点发生联系,作为选线的“终点”。成本路径工具支持一个源及多个源作为参数输入,故而能够将全部项目作为多个源输入,参与运算。由于运算规则所限,在需要通过路径上补点,并与项目节点一起作为终止点参与选线运算。例如,选线结果未经过某陡崖一侧,但此处景象较为特殊,设计师有意识希望道路能够将游人引导至此地,营造变化的游赏视觉体验,便可根据情况在该处进行补点。
3.5 成本距离分析
将综合成本图以及道路起始点作为参数输入成本距离工具,能够得出与起始点相关的成本加权距离与成本加权方向图纸,分别标识出返回至最近源位置的各像元的累积成本及从成本距离栅格中的每个像元返回源时的行进方向。路径距离工具与成本距离相比需要更多的参数输入,如表面栅格、与垂直系数计算相关的交角限制值和SLOPE值等。这些输入的参数有助于进一步对选线路径按照景园规划设计要求进行约定。
3.6 最优路线生成
根据输入的终止点个数,最优路线生成分为两点间及多点间的最优路径计算。景园环境中的建设项目,包括景观与建筑节点均需与主入口相连,部分可达次级入口。建设项目往往不止一项,如若人为决定参与选线的节点顺序,依次进行两点最优路径的计算,选择得出的路径表达了过强的人为意志。此外,在此操作生成全区域的路网对应的工作量巨大,尤其是对于尺度较大的风景区规划而言,涉及的道路节点众多,难以凭借依次两点选线生成路网。因此,本文采取多点同时计算,不仅符合项目节点与出入口的交通逻辑关系,而且便于内部路网的形成。由于每一个项目节点均会生成到达起始点的路径,因此项目的个数决定了路径的条数,对应了所形成的路网密度。
3.7 路径的筛选与优化
现有计算方式与条件下通过算法输出的选线路径,难以完全满足最终的路网形态要求。因此,需进行人工的筛选及优化,剔除多余路径,优化线型。为使道路呈环,部分节点必须同时与2个以上的其他节点直接发生联系。而单次的选线计算仅会建立两点间的联系,所以需要进行多次的计算。由于栅格计算的特点,成本路径算法输出的路径由连续的栅格组成,通过矢量输出之后可利用“平滑线”等工具结合人工对线形进行优化,以生成最终的道路线形。
4 参数化风景环境道路选线模型的应用
基于综合成本最短路径算法模型进行路径选择有2种算法途径,第一种是成本路径算法,另一种为路径距离算法。两者之间的区别在于运用的ArcGIS运算工具不同。就参数而言,路径距离算法输入的参数较之成本路径算法更多,因此能够对运算给予更多的限定条件(表2)。风景环境景点众多,道路选线必然面临的是一个多点的选线问题。为避免过大的工作量及人为意志干扰,本文针对风景环境道路选线特点提出“‘1+N’多点多次选线方法”,即将多点同时作为选线的终点,形成参数,一次性输入,进行道路的选线运算。
结合南京以牛首山景区北部片区规划,笔者采取基于“1+N”多点多次选线方法,选取路径距离算法,对参数化风景环境道路选线模型的应用加以展示。
牛首山景区北部地区的道路选线影响因子为坡度、水域以及起伏度。首先,通过德尔菲法、层次分析法等评价方法确定以上影响因子的权重;其次,利用GIS软件的重分类功能,将各因子无量纲化并赋值;最后,进行叠加分析得到综合成本图(图3)。
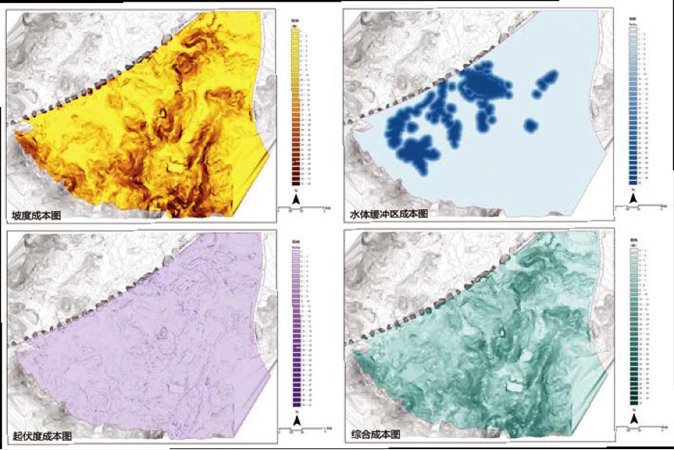
图3 综合成本图的生成
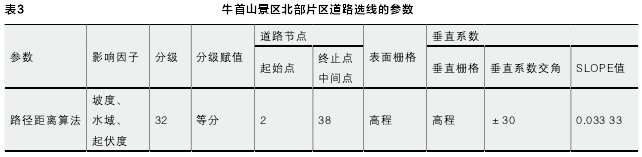
风景环境中,景观节点均需被路网串联,以供游人到达,故而这些节点均与路网发生关系,成为道路选线的“控制点”,即道路的起始点、中间点以及终止点。根据上位规划及项目定位,该区域存在多个出入口,任一景观节点须能够顺利地从区域主入口进入。故而本文的道路选线模型将区域主入口所在位置作为起始点参数输入,其余景观节点作为“中间点”及“终止点”参数。利用路径距离算法,本次选线的参数如表3所示,得到图4展示的选线结果。由于栅格图计算得出的选线线型为折线,不能够直接作为实际选线结果,因而需要将其曲线化以满足道路设计的要求。借助ArcGIS工具对线型进行曲线化处理,并对不尽合理的部分加以人工筛选及优化得出最终的选线形态。在全部路网路径生成的基础上,分出主次道路,选线路径即为道路的中心线。最后,通过CAD软件的绘制与调整,得出整个设计区域内的路网(图5)。
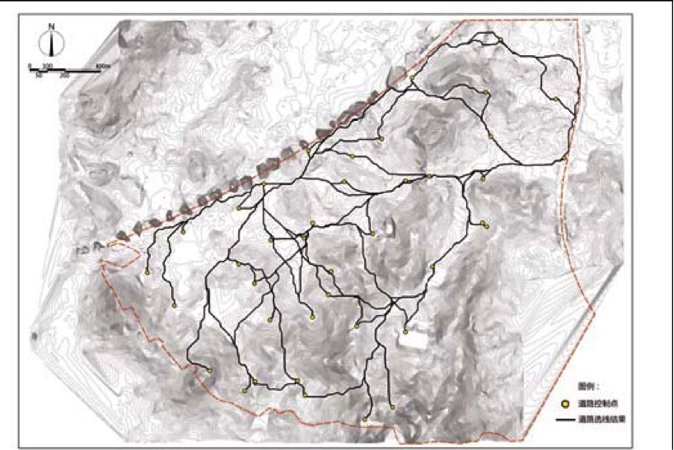
图4 道路选线结果
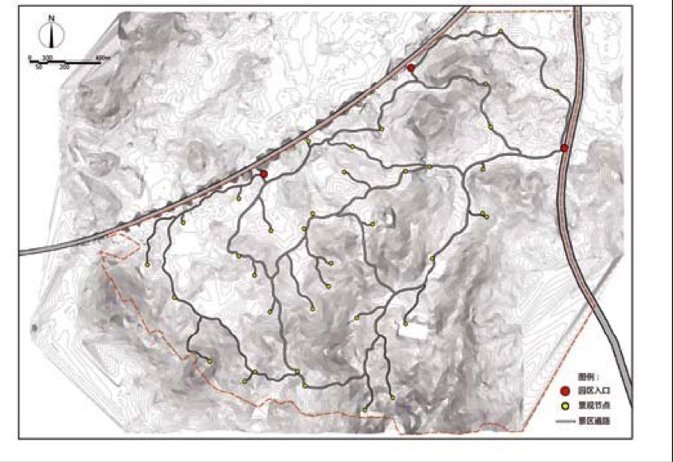
图5 最终生成的路网
5 结语:参数化风景环境道路选线的意义与价值
科学技术极大地推动了风景园林理论与实践的进步,参数化风景环境道路选线方法较之于传统凭经验的选线方法更为科学、准确、高效。区别于传统方法的主观性、随机性与模糊性,基于计算机技术的选线方法对于参数的引入使得设计过程变得精确、可控,不仅可以同时兼顾多种设计目标,而且能够实现基于耦合原理的景园规划设计要求。
注:文中图片均由作者提供。
作者简介:
袁旸洋/1987年生/女/江苏南京人/东南大学建筑学院风景园林专业在读博士研究生(南京 210096)
成玉宁/1962年生/男/江苏南京人/博士/东南大学建筑学院教授,博士生导师,东南大学风景园林学科带头人,景观学系主任,东南大学景观规划设计研究所所长/国务院学位委员会风景园林学科评议组成员/研究方向为风景园林规划设计、景观建筑设计、景园历史与理论、数字景观及其技术/本刊编委(南京 210096)
 《中国园林》2015第7期导读
《中国园林》2015第7期导读
Leave a Reply